Nội dung ôn tập Toán Lớp 10 - Chủ đề: Hệ thức lượng trong tam giác

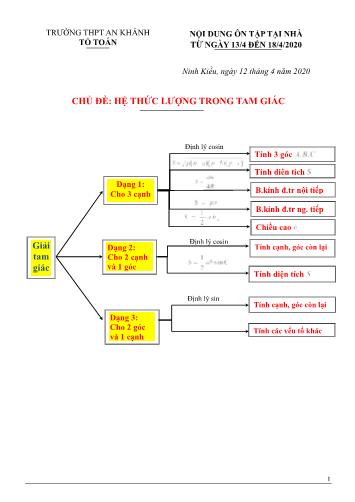
1 
TRƯỜNG THPT AN KHÁNH 
TỔ TOÁN 
NỘI DUNG ÔN TẬP TẠI NHÀ 
TỪ NGÀY 13/4 ĐẾN 18/4/2020 
Ninh Kiều, ngày 12 tháng 4 năm 2020 
CHỦ ĐỀ: HỆ THỨC LƯỢNG TRONG TAM GIÁC 
Giải 
tam 
giác 
Dạng 2: 
Cho 2 cạnh 
và 1 góc 
Dạng 1: 
Cho 3 cạnh 
Dạng 3: 
Cho 2 góc 
và 1 cạnh 
B.kính đ.tr nội tiếp 
Tính 3 góc 
Tính diện tích 
B.kính đ.tr ng. tiếp 
Chiều cao 
Định lý cosin 
Tính cạnh, góc còn lại 
Tính diện tích 
Định lý cosin 
Tính cạnh, góc còn lại 
Tính các yếu tố khác 
Định lý sin 
2 
BÀI TẬP TỰ LUẬN 
Bài 1. (Dạng toán 1) Cho tam giác ABC biết các cạnh 52,1 ; 85 a cm b cm và 
54 .c cm 
 a) Tính các góc , , .A B C 
 b) Tính diện tích tam giác ABC 
 c) Tính bán kính đường tròn nội tiếp, ngoại tiếp tam giác ABC và chiều cao tam giác 
ABC kẻ từ đỉnh .A 
Lời giải 
a) Áp dụng định lý cosin 
2 2 2
22 22 2 2
0
2 cos
85 54 52,1
cos 0,88089
2 2.85.54
36
a b c bc A
b c a
A
bc
A
22 22 2 2
0
54 52,1 85
cos 0,283
2 2.54.52,1
106 26
a c b
B
ac
B
0 0180 ( ) 37 34C A B 
Vậy : 036A , 0106 26B , 037 34C 
 b) Nửa chu vi tam giác: 
52,1 85 54
95,55
2 2
a b c
p
 Diện tích tam giác ABC là 
2( )( )( ) 1349S p p a p b p c cm 
c) Bán kính đường tròn nội tiếp tam giác ABC 
1349
. 14,1
95,55
S
S p r r cm
p
 Bán kính đường tròn ngoại tiếp tam giác ABC 
52,1.85.54
44,3
4 4 4.1349
abc abc
S R cm
R S
Chiều cao ah kẻ từ đỉnh A của tam giác ABC 
1 2 2.1349
51,8
2 52,1
a a
S
S ah h cm
a
Bài 2. (Dạng toán 2) Cho tam giác ABC có  06, 8, 60b c A . 
 a) Tính độ dài cạnh a và hai góc , .B C 
 b) Tính diện tích tam giác ABC 
 c) Tính bán kính đường tròn ngoại tiếp tam giác ABC 
Lời giải 
a) Áp dụng định lý cosin 
3 
2 2 2
2 2 0
2 2 0
2 cos
6 8 2.6.8.cos60
6 8 2.6.8.cos60 2 13
a b c bc A
a
 Tính số đo góc ,B C 
2
2 22 2 2
0
2 13 8 6 10 13
cos
2 392.2 13.8
22 24
a c b
B
ac
B
0 0180 ( ) 97 36C A B 
Vậy : 0 02 13; 22 24 ; 97 36a B C 
 b) Diện tích tam giác ABC là 
 0
1 1
.sin .6.8.sin 60 12 3
2 2
S bc A 
 c) Tính bán kính đường tròn ngoại tiếp tam giác ABC 
 Áp dụng định lý sin: 
0
2 13 2 39
2
sin 2.sin 32.sin 60
a a
R R
A A
Bài 3. (Dạng toán 3) Cho tam giác ABC có góc 0,60A góc 045 , 2.B b 
 a) Tính số đo góc ,C độ dài các cạnh , .a c 
b) Tính bán kính đường tròn ngoại tiếp và diện tích tam giác ABC . 
Lời giải 
a) Ta có: 
 0 0180 75C A B 
 Áp dụng định lý sin: 
0 0 0
2
sin sin sin sin 60 sin 45 sin 75
a b c a c
A B C
0
0
2.sin 60
6
sin 45
a 
 Và 
0
0
2.sin75
1 3
sin 45
c 
b) Bán kính đường tròn ngoại tiếp 
0
6
2 2
sin 2.sin 2.sin 60
a a
R R
A A
 Diện tích tam giác ABC : 
 01 1 6 2 2sin 2. 1 3 .sin 75
2 2 2
S bc A
  
BÀI TẬP TRẮC NGHIỆM 
4 
DẠNG TOÁN 1: 
Câu 1. Cho tam giác ,ABC biết 24, 13, 15.a b c Số đo gần đúng góc A của tam 
giác ABC là 
A. 033 34 '. B. 0117 49 '. C. 028 37 '. D. 058 24'. 
Câu 2. Cho tam giác ,ABC biết 13, 14, 15.a b c Số đo gần đúng góc B của tam 
giác ABC là 
A. 059 49 '. B. 053 7'. C. 059 29 '. D. 062 22 '. 
Câu 3. Cho tam giác ,ABC có 6, 8, 10.a b c Diện tích của tam giác là 
 A. 48. B. 24. C. 12. D. 30. 
Câu 4. Một tam giác có độ dài ba cạnh là 26,28,30. Bán kính đường tròn nội tiếp của 
tam giác là 
 A. 16. B. 8. C. 4. D.4 2. 
Câu 5. Cho tam giác ,ABC có 13, 14, 15.a b c Độ dài bán kính đường tròn ngoại 
tiếp của tam giác trên là 
 A. 
65
.
8
 B. 130. C. 8. D. 
17
.
2
Câu 6. Cho tam giác ,ABC có 6, 4 2, 2.a b c Gọi M là điểm trên cạnh BC sao 
cho 3BM . Độ dài đoạn AM là 
A. 9 . B. 9. C. 3. D. 
1
108 .
2
DẠNG TOÁN 2: 
Câu 7. Cho tam giác ,ABC có 060 , 8, 5.B a c Độ dài cạnh b bằng 
 A. 7. B. 129. C. 49. D. 129. 
Câu 8. Cho tam giác ,ABC có 04, 5, 150 .a c B Diện tích của tam giác là 
A.5 3. B. 5. C. 10. D. 10 3. 
Câu 9. Cho tam giác ,ABC có b = 7; c = 5, 
3
cos
5
 A . Đường cao ah của tam giác ABC 
là 
A. 
7 2
.
2
 B. 8. C.8 3. D.80 3. 
Câu 10. Cho tam giác ,ABC có 8, 10,a b góc 060 .C Độ dài cạnh c là 
A. 3 21c . B. 7 2c . C. 2 11c . D. 2 21c . 
Câu 11. Cho tam giác ,ABC có  08, 3, 60 .a c B Độ dài cạnh b bằng 
A. 49. B. 97. C. 7. D. 61. 
DẠNG TOÁN 3: 
Câu 12. Cho tam giác ,ABC có  0 045 , 75C B . Số đo góc A của tam giác là 
5 
 A. 065 .A B. 070 .A C. 060 .A D. 075 .A 
Câu 13. Cho tam giác ,ABC có  0 016,8; 56 13'; 71 .a B C Độ dài cạnh c gần bằng giá 
trị nào sau đây? 
A. 29,9. B. 14,1. C. 17,5. D. 19,9. 
Câu 14. Cho tam giác ,ABC có  0 068 12'; 34 44',A B cạnh 117.AB Độ dài cạnh AC 
là 
 A. 68. B. 168. C. 118. D.200. 
DẠNG TOÁN: Các bài toán thực tế áp dụng hệ thức lương trong tam giác 
Câu 15. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. 
Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới 
một góc 78 24'.o Biết 250 , 120 .CA m CB m Khoảng cách AB bằng bao nhiêu? 
A. 266 .m B. 255 .m C. 166 .m D. 298 .m 
Câu 16. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí ,A đi thẳng theo hai hướng tạo với 
nhau một góc 060 . Tàu thứ nhất chạy với tốc độ 30 /km h , tàu thứ hai chạy với 
tốc độ 40 / .km h Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu ?km 
A. 13 .km B. 15 13 .km C. 10 13 .km D. 15 .km 
Câu 17. Từ một đỉnh tháp chiều cao 80 ,CD m người ta nhìn hai điểm A và B trên 
mặt đất dưới các góc nhìn là 072 12' và 034 26'.Ba điểm , ,A B D thẳng hàng. Tính 
khoảng cách .AB 
A. 71 .m B. 91 .m C. 79 .m D. 40 .m 
Câu 18. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. 
Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một 
góc 056 16' . Biết 200CA m , 180CB m . Khoảng cách AB bằng bao nhiêu ? 
A. 163 .m B. 224 .m C. 112 .m D. 168 .m