Đề kiểm tra Học kì I môn Toán Lớp 11 năm học 2012- 2013 (Có đáp án)

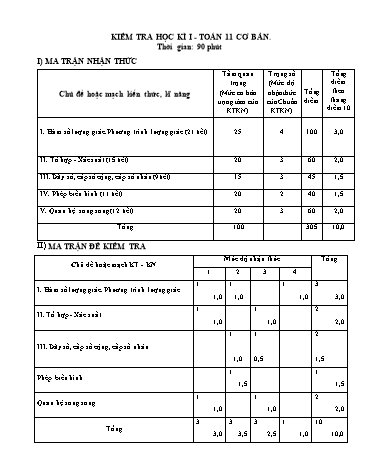
KIỂM TRA HỌC KÌ I - TOÁN 11 CƠ BẢN.
Thời gian: 90 phút
I) MA TRẬN NHẬN THỨC
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm quan trọng
(Mức cơ bản trọng tâm của KTKN)
Trọng số
(Mức độ nhận thức của Chuẩn KTKN)
Tổng điểm
Tổng điểm theo thang điểm 10
I. Hàm số lượng giác. Phương trình lượng giác (21 tiết)
25
4
100
3,0
II. Tổ hợp - Xác suất (15 tiết)
20
3
60
2,0
III. Dãy số, cấp số cộng, cấp số nhân (9tiết)
15
3
45
1,5
IV. Phép biến hình (11 tiết)
20
2
40
1,5
V. Quan hệ song song (12 tiết)
20
3
60
2,0
Tổng
100
305
10,0
II) MA TRẬN ĐỀ KIỂM TRA 
Chủ đề hoặc mạch KT - KN
Mức độ nhận thức
Tổng
1
2
3
4
I. Hàm số lượng giác. Phương trình lượng giác
1
1,0
1
1,0
1
1,0
3
3,0
II. Tổ hợp - Xác suất
1
1,0
1
1,0
2
2,0
III. Dãy số, cấp số cộng, cấp số nhân
1
 1,0
1
 0,5
2
 1,5
Phép biến hình
1
1,5
1
1,5
Quan hệ song song
1
1,0
1
1,0
2
2,0
Tổng
3
3,0
3
3,5
3
2,5
1
1,0
10
10,0
III) BẢNG MÔ TẢ TIÊU CHÍ ĐỀ KIỂM TRA MÔN TOÁN KHỐI 11 
HỌC KỲ I - NĂM HỌC 2012 - 2013
Câu 1 (1,0đ). Tìm tập xác định của các hàm số có chứa các biểu thức lượng giác (Dạng như bài tập 2a, c trang 17 SGK ĐS và GT11) hoặc giải một phương trình lượng giác cơ bản. 
Câu 2a(1,0đ). Giải một phương trình lượng giác thường gặp. 
Câu 2b (1,0đ). Giải một phương trình lượng giác khác.
Câu 3a (1,0đ). Áp dụng quy tắc cộng, quy tắc nhân, hoán vị, chỉnh hợp, tổ hợp (Dạng bài tập 1, 2, 3, 6 trang 54,55 SGK ĐS và GT 11) hoặc tính xác suất theo định nghĩa xác suất cổ điển). 
Câu 3b (1,0đ). Tìm hệ số của xn trong khai triển nhị thức Niu tơn (Dạng bài tập 2 trang 58 SGK ĐS và GT11).
Câu 4a (1,0đ). Tìm vài số hạng hoặc tính tổng n số hạng đầu của một cấp số cộng hoặc cấp số nhân khi biết số hạng số hạng đầu và công sai (công bội). 
Câu 4b (0,5đ). Tìm cấp số cộng hoặc cấp số nhân khi biết mối quan hệ giữa các số hạng của chúng. 
Câu 5 (1,5đ). Xác định ảnh của hình (Điểm, đường thẳng, đường tròn) qua phép một phép biến hình (bằng phương pháp tọa độ). 
Câu 6a(1,0đ). Vẽ được hình và xác định được giao tuyến của hai mặt phẳng có một điểm chung cho trước.
Câu 6b (1,0đ). Tìm thiết diện khi cắt hình chóp bởi một mặt phẳng có sử dụng tính chất song song của đường thẳng và mặt phẳng (Dạng bài tập 2, 3 trang 63 SGK HH11).
IV) ĐỀ KIỂM TRA HỌC KÌ I.
Bài 1. (1,0điểm) Tìm tập xác định của các hàm số:.
Bài 2. (2,0 điểm) Giải các phương trình lượng giác:
a) 	b) 
Bài 3. (1,5 điểm) 
a) Tính tổng 10 số hạng đầu của một cấp số nhân có số hạng đầu , công bội .
b) Tìm cấp số cộng có: .
Bài 4. (2,0 điểm) 
a) Cho 2 đường thẳng song song và . Trên lấy 15 điểm phân biệt, trên lấy 35 điểm phân biệt. Tính số tam giác có các đỉnh là 3 trong số 50 điểm đã cho trên và .
b) Tìm hệ số của trong khai triển của nhị thức Niutơn: .
Bài 5. (1,5 điểm) Trong mặt phẳng tọa độ Oxy, cho đường thẳng ; vectơ . Tìm ảnh của đường thẳng qua phép tịnh tiến theo vectơ .
Bài 6. (2,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của AD, là mặt phẳng qua M và song song với BD, SC.
1) Tìm giao tuyến của (SAB) và (SCD); (SAC) và (SBD).
2) Xác định thiết diện của hình chóp cắt bởi mp.
V) ĐÁP ÁN-BIỂU ĐIỂM
Câu
Đáp án
Điểm
1
ĐKXĐ: 
0,5
Vậy tập xác định của hàm số: 
0,5
2
a) ĐKXĐ: 
0,25
0,25
 (thỏa mãn điều kiện)
Kết luận: 
0,5
b) 
0,5
Kết luận: hoặc 
0,5
3
a) 
0,5
b) 
0,5
0,5
4
a) Theo đề bài ta có: 
- Số tam giác được tạo thành khi chọn một đỉnh thuộc và hai đỉnh thuộc là: 
- Số tam giác được tạo thành khi chọn hai đỉnh thuộc và một đỉnh thuộc là: .
0,5
Vậy, số tam giác được tạo thành thoả mãn đề bài là: (tam giác).
0,5
b) .
0,5
Ta có: 
Vậy, hệ số của trong khai triển đã cho là: .
0,5
5
Gọi ảnh của đường thẳng qua phép tịnh tiến theo vectơ là đường thẳng .
Giả sử . Khi đó là ảnh của điểm qua phép tịnh tiến theo vectơ phải thoả mãn . 
0,5
Ta có : .
0,5
Vậy đường thẳng cần tìm có phương trình: .
0,5
6
0,5
a)* Gọi . 
+) Ta có .
+)
Vậy a thoả mãn 
0,25
* Gọi . 
+) Ta có .
+) Trong mp (ABCD) gọi khi đó 
Vậy b thoả mãn . Tức là có: 
0,25
b) Chứng minh và kết luận được thiết diện là tam giác MIG như hình vẽ.
1,0