Chuyên đề ôn thi THPT QG Toán 12 - Chủ đề: Mặt nón, mặt trụ, mặt cầu

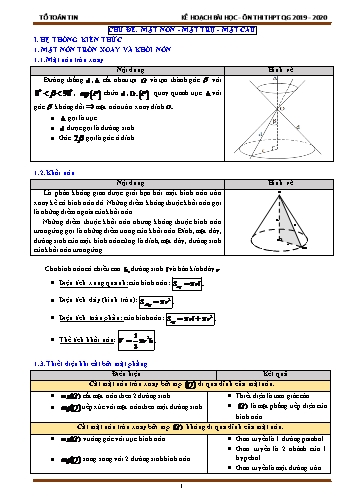
CHỦ ĐỀ. MẶT NÓN - MẶT TRỤ - MẶT CẦU
I. HỆ THỐNG KIẾN THỨC
1. MẶT NÓN TRÒN XOAY VÀ KHỐI NÓN
1.1. Mặt nón tròn xoay
Nội dung
Hình vẽ
Đường thẳng , cắt nhau tại và tạo thành góc với , chứa , quay quanh trục với góc không đổi mặt nón tròn xoay đỉnh 
 gọi là trục.
 được gọi là đường sinh.
Góc gọi là góc ở đỉnh.
1.2. Khối nón
Nội dung
Hình vẽ
Là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó. Những điểm không thuộc khối nón gọi là những điểm ngoài của khối nón. 
Những điểm thuộc khối nón nhưng không thuộc hình nón tương ứng gọi là những điểm trong của khối nón. Đỉnh, mặt đáy, đường sinh của một hình nón cũng là đỉnh, mặt đáy, đường sinh của khối nón tương ứng.
Cho hình nón có chiều cao đường sinh và bán kính đáy.
Diện tích xung quanh: của hình nón: 
Diện tích đáy (hình tròn):
Diện tích toàn phần: của hình nón: 
Thể tích khối nón: 
1.3. Thiết diện khi cắt bởi mặt phẳng
Điều kiện
Kết quả
Cắt mặt nón tròn xoay bởi mp đi qua đỉnh của mặt nón.
 cắt mặt nón theo 2 đường sinh.
tiếp xúc với mặt nón theo một đường sinh.
Thiết diện là tam giác cân.
 là mặt phẳng tiếp diện của hình nón.
Cắt mặt nón tròn xoay bởi mp không đi qua đỉnh của mặt nón.
 vuông góc với trục hình nón.
 song song với 2 đường sinh hình nón.
 song song với 1 đường sinh hình nón.
Giao tuyến là 1 đường parabol.
Giao tuyến là 2 nhánh của 1 hypebol.
Giao tuyến là một đường tròn.
2. MẶT TRỤ TRÒN XOAY
2.1. Mặt trụ
Nội dung
Hình vẽ
Trong mặt phẳng cho hai đường thẳng và song song với nhau, cách nhau một khoảng bằng . Khi quay mặt phẳng xung quanh thì đường thẳng sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay, gọi tắt là mặt trụ.
Đường thẳng gọi là trục.
Đường thẳng là đường sinh.
 là bán kính của mặt trụ đó.
2.2. Hình trụ tròn xoay và khối trụ tròn xoay
Nội dung
Hình vẽ
Ta xét hình chữ nhật . Khi quay hình chữ nhật xung quanh đường thẳng chứa một cạnh nào đó, chẳng hạn cạnh AB thì đường gấp khúc sẽ tạo thành một hình gọi là hình trụ tròn xoay, hay gọi tắt là hình trụ.
Khi quay quanh hai cạnh và sẽ vạch ra hai hình tròn bằng nhau gọi là hai đáy của hình trụ, bán kính của chúng gọi là bán kính của hình trụ.
Độ dài đoạn gọi là độ dài đường sinh của hình trụ.
Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh khi quay xung quanh gọi là mặt xung quanh của hình trụ.
Khoảng cách giữa hai mặt phẳng song song chứa hai đáy là chiều cao của hình trụ.
Khối trụ tròn xoay hay khối trụ là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ tròn xoay đó. Những điểm không thuộc khối trụ gọi là những điểm ngoài của khối trụ. Những điểm thuộc khối trụ nhưng không thuộc hình trụ tương ứng gọi là những điểm trong của khối trụ. Mặt đáy, chiều cao, đường sinh, bán kính của một hình trụ cũng là mặt đáy, chiều cao, đường sinh, bán kính của khối trụ tương ứng.Hình trụ có chiều cao đường sinh và bán kính đáy 
Diện tích xung quanh: 
Diện tích toàn phần: 
Thể tích: 
3. MẶT CẦU – KHỐI CẦU
3.1. Mặt cầu
Nội dung
Hình vẽ
Cho điểm cố định và một số thực dương . 
Tập hợp tất cả những điểm trong không gian cách một khoảng được gọi là mặt cầu tâm bán kính 
Kí hiệu: Khi đó: 
3.2. Vị trí tương đối giữa mặt cầu và mặt phẳng
Cho mặt cầu và mặt phẳng . Gọi là hình chiếu vuông góc của lên là khoảng cách từ đến mặt phẳng . Khi đó:
Mặt cầu và mặt phẳng không có điểm chung.
Mặt phẳng tiếp xúc mặt cầu: là mặt phẳng tiếp diện của mặt cầu và tiếp điểm.
Mặt phẳng cắt mặt cầu theo thiết diện là đường tròn có tâmvà bán kính 
Lưu ý:
Khi mặt phẳng đi qua tâm của mặt cầu thì mặt phẳng được gọi là mặt phẳng kính và thiết diện lúc đó được gọi là đường tròn lớn.
3.3. Vị trí tương đối giữa mặt cầu và đường thẳng
Cho mặt cầu và đường thẳng . Gọi là hình chiếu của lên . Khi đó:
 không cắt mặt cầu.
 tiếp xúc với mặt cầu.
: Tiếp tuyến của 
tiếp điểm.
 cắt mặt cầu tại hai điểm phân biệt.
Lưu ý: Trong trường hợp cắt tại 2 điểm thì bán kính của được tính như sau: 
3.4. Đường kinh tuyến và vĩ tuyến của mặt cầu
Nội dung
Hình vẽ
Giao tuyến của mặt cầu với nửa mặt phẳng có bờ là trục của mặt cầu được gọi là kinh tuyến.
Giao tuyến (nếu có) của mặt cầu với các mặt phẳng vuông góc với trục được gọi là vĩ tuyến của mặt cầu.
Hai giao điểm của mặt cầu với trục được gọi là hai cực của mặt cầu
* Mặt cầu nội tiếp, ngoại tiếp hình đa diện:
Nội dung
Hình vẽ
Mặt cầu nội tiếp hình đa diện nếu mặt cầu đó tiếp xúc với tất cả các mặt của hình đa diện. Còn nói hình đa diện ngoại tiếp mặt cầu.
Mặt cầu ngoại tiếp hình đa diện nếu tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu. Còn nói hình đa diện nội tiếp mặt cầu.
Mặt cầu tâm bán kính ngoại tiếp hình chóp khi và chỉ khi
Cho mặt cầu 
Diện tích mặt cầu:.
Thể tích khối cầu:.
4. MỘT SỐ DẠNG TOÁN VÀ CÔNG THỨC GIẢI
4.1. Bài toán mặt nón
4.1.1.Dạng 1. Thiết diện của hình nón cắt bởi một mặt phẳng
Nội dung
Hình vẽ
Thiết diện qua trục của hình nón là tam giác cân.
Thiết diện qua đỉnh của hình nón là những tam giác cân có hai cạnh bên là hai đường sinh của hình nón.
Thiết diện vuông góc với trục của hình nón là những đường tròn có tâm nằm trên trục của 
hình nón.
4.1.2. Dạng 2. Bài toán liên quan đến thiết diện qua đỉnh của hình nón
Cho hình nón có chiều cao là , bán kính đáy và đường sinh . 
Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 
Nội dung
Hình vẽ
Gọi là trung điểm của Khi đó:
Góc giữa và là góc.
Góc giữa và là góc.
Diện tích thiết diện
4.1.3. Dạng 3. Bài toán hình nón ngoại tiếp và nội tiếp hình chóp
Nội dung
Hình vẽ
Hình nón nội tiếp hình chóp đều là hình nón có đỉnh là , đáy là đường tròn nội tiếp hình vuông . 
Khi đó hình nón có:
Bán kính đáy , 
Đường cao , đường sinh 
Hình chóp tứ giác đều
Hình nón ngoại tiếp hình chóp đều là hình nón có đỉnh là , đáy là đường tròn ngoại tiếp hình vuông . 
Khi đó hình nón có:
Bán kính đáy: 
Chiều cao: 
Đường sinh: 
Hình chóp tứ giác đều
Hình nón nội tiếp hình chóp đều là hình nón có đỉnh là , đáy là đường tròn nội tiếp tam giác 
Khi đó hình nón có 
Bán kính đáy: 
Chiều cao: 
Đường sinh: 
Hình chóp tam giác đều
Hình nón ngoại tiếp hình chóp đều là hình nón có đỉnh là , đáy là đường tròn ngoại tiếp tam giác 
Khi đó hình nón có:
Bán kính đáy: 
Chiều cao: 
Đường sinh: 
Hình chóp tam giác đều
4.1.4. Dạng 4. Bài toán hình nón cụt
Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần mặt phẳng nằm trong hình nón là một hình tròn. Phần hình nón nằm giữa hai mặt phẳng nói trên được gọi là hình nón cụt.
Nội dung
Hình vẽ
Khi cắt hình nón cụt bởi một mặt phẳng song song với đáy thì được mặt cắt là một hình tròn.
Khi cắt hình nón cụt bởi một mặt phẳng song song với trục thì được mặt cắt là một hình thang cân.
Cho hình nón cụt có lần lượt là bán kính đáy lớn, bán kính đáy nhỏ và chiều cao.
Diện tích xung quanh của hình nón cụt: 
Diện tích đáy (hình tròn): 
Diện tích toàn phần của hình nón cụt: 
Thể tích khối nón cụt:
4.1.5. Dạng 5. Bài toán hình nón tạo bởi phần còn lại của hình tròn sau khi cắt bỏ đi hình quạt
Nội dung
Hình vẽ
Từ hình tròn cắt bỏ đi hình quạt Độ dài cung bằng Phần còn lại của hình tròn ghép lại được một hình nón. Tìm bán kính, chiều cao và độ dài đường sinh của hình nón đó.
Hình nón được tạo thành có
4.2. Một số dạng toán và công thức giải bài toán mặt trụ
4.2.1. Dạng 1. Thiết diện của hình trụ cắt bởi một mặt phẳng
Nội dung
Hình vẽ
Thiết diện vuông góc trục là một đường tròn bán kính 
Thiết diện chứa trục là một hình chữ nhật trong đó và . Nếu thiết diện qua trục là một hình vuông thì .
Thiết diện song song với trục và không chứa trục là hình chữ nhật có khoảng cách tới trục là: 
4.2.2. Dạng 2. Thể tích khối tứ diện có 2 cạnh là đường kính 2 đáy
Nội dung
Hình vẽ
Nếu như và là hai đường kính bất kỳ trên hai đáy của hình trụ thì: 
* Đặc biệt: Nếu và vuông góc nhau thì:
.
4.2.3. Dạng 3. Xác định góc khoảng cách
Nội dung
Hình vẽ
Góc giữa và trục : 
Khoảng cách giữa và trục : 
.
Nếu là một hình vuông nội tiếp trong hình trụ thì đường chéo của hình vuông cũng bằng đường chéo của hình trụ. 
Nghĩa là cạnh hình vuông:
.
4.2.4. Dạng 4. Xác định mối liên hệ giữa diện tích xung quanh, toàn phần và thể tích khối trụ trong bài toán tối ưu
Nội dung
Hình vẽ
Một khối trụ có thể tích không đổi.
Tìm bán kính đáy và chiều cao hình trụ để diện tích toàn phần nhỏ nhất:
Tìm bán kính đáy và chiều cao hình trụ để diện tích xung quanh cộng với diện tích 1 đáy và nhỏ nhất:
4.2.5. Dạng 5. Hình trụ ngoại tiếp, nội tiếp một hình lăng trụ đứng
Cho hình lăng trụ tam giác đêu nội tiếp trong một hình trụ. Thể tích khối lăng trụ là thì thể tích khối trụ là 
Cho hình lăng trụ tứ giác đêu ngoại tiếp trong một hình trụ. Diện tích xung quanh hình trụ là thì diện tích xung quanh của hình lăng trụ là 
5. MỘT SỐ DẠNG TOÁN VÀ CÔNG THỨC GIẢI BÀI TOÁN MẶT CẦU
5.1. Mặt cầu ngoại tiếp khối đa diện
5.1.1. Các khái niệm cơ bản
Trục của đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp của đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy Bất kì một điểm nào nằm trên trục của đa giác thì cách đều các đỉnh của đa giác đó.
Đường trung trực của đoạn thẳng: là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
 Bất kì một điểm nào nằm trên đường trung trực thì cách đều hai đầu mút của đoạn thẳng.
Mặt trung trực của đoạn thẳng: là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
 Bất kì một điểm nào nằm trên mặt trung trực thì cách đều hai đầu mút của đoạn thẳng.
5.1.2. Tâm và bán kính mặt cầu ngoại tiếp hình chóp
Tâm mặt cầu ngoại tiếp hình chóp: là điểm cách đều các đỉnh của hình chóp. Hay nói cách khác, nó chính là giao điểm của trục đường tròn ngoại tiếp mặt phẳng đáy và mặt phẳng trung trực của một cạnh bên hình chóp.
Bán kính: là khoảng cách từ đến các đỉnh của hình chóp.
5.1.3. Cách xác định tâm và bán kính mặt cầu của một số hình đa diện 
5.1.3.1. Hình hộp chữ nhật, hình lập phương
Nội dung
Hình vẽ
Tâm: trùng với tâm đối xứng của hình hộp chữ nhật (hình lập phương) Tâm là , là trung điểm của .
Bán kính: bằng nửa độ dài đường chéo hình hộp chữ nhật (hình lập phương).
Bán kính: .
5.1.3.2. Hình lăng trụ đứng có đáy nội tiếp đường tròn
Nội dung
Hình vẽ
Xét hình lăng trụ đứng , trong đó có 2 đáyvà nội tiếp đường tròn và . Lúc đó, mặt cầu nội tiếp hình lăng trụ đứng có:
Tâm: với là trung điểm của .
Bán kính: .
5.1.3.3. Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông
Nội dung
Hình vẽ
Hình chóp có .
Tâm: là trung điểm của.
Bán kính: .
Hình chóp có
.
Tâm: là trung điểm của.
Bán kính: .
5.1.3.4. Hình chóp đều
Nội dung
Hình vẽ
Cho hình chóp đều
Gọi là tâm của đáylà trục của đáy.
Trong mặt phẳng xác định bởi và một cạnh bên, chẳng hạn như , ta vẽ đường trung trực của cạnh là cắt tại và cắt tại là tâm của mặt cầu.
Bán kính: 
Ta có: Bán kính:
5.1.3.5. Hình chóp có cạnh bên vuông góc với mặt phẳng đáy
Nội dung
Hình vẽ
Cho hình chóp có cạnh bên và đáy nội tiếp được trong đường tròn tâm . 
Tâm và bán kính mặt cầu ngoại tiếp hình chóp được xác định như sau: 
Từ tâm ngoại tiếp của đường trònđáy, ta vẽ đường thẳng vuông góc với tại .
Trong , ta dựng đường trung trực của cạnh, cắttại, cắt tại là tâm mặt cầu ngoại tiếp hình chóp và bán kính
Tìm bán kínhTa có: là hình chữ nhật.
Xét vuông tại có: 
.
5.1.3.6. Hình chóp khác
Dựng trục của đáy.
Dựng mặt phẳng trung trực của một cạnh bên bất kì.
 là tâm mặt cầu ngoại tiếp hình chóp.
Bán kính: khoảng cách từ đến các đỉnh của hình chóp.
5.1.3.7. Đường tròn ngoại tiếp một số đa giác thường gặp
Khi xác định tâm mặt cầu, ta cần xác định trục của mặt phẳng đáy, đó chính là đường thẳng vuông góc với mặt phẳng đáy tại tâm O của đường tròn ngoại tiếp đáy. Do đó, việc xác định tâm ngoại O là yếu tố rất quan trọng của bài toán.
∆ vuông: O là trung điểm của cạnh huyền.
O
Hình vuông: O là giao điểm 2 đường chéo.
O
Hình chữ nhật: O là giao điểm của hai đường chéo.
O
O
∆ đều: O là giao điểm của 2 đường trung tuyến (trọng tâm).
∆ thường: O là giao điểm của hai đường trung trực của hai cạnh ∆.
O
5.2. Kỹ thuật xác định mặt cầu ngoại tiếp hình chóp
Nội dung
Hình vẽ
Cho hình chóp (thoả mãn điều kiện tồn tại mặt cầu ngoại tiếp). Thông thường, để xác định mặt cầu ngoại tiếp hình chóp ta thực hiện theo hai bước:
Bước 1: 
Xác định tâm của đường tròn ngoại tiếp đa giác đáy. Dựng : trục đường tròn ngoại tiếp đa giác đáy.
Bước 2: 
Lập mặt phẳng trung trực của một cạnh bên. 
Lúc đó 
Tâm của mặt cầu: 
Bán kính: . Tuỳ vào từng trường hợp.
5.3. Kỹ năng xác định trục đường tròn ngoại tiếp đa giác đáy
5.3.1. Trục đường tròn ngoại tiếp đa giác đáy
Nội dung
Hình vẽ
Định nghĩa
Trục đường tròn ngoại tiếp đa giác đáy là đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và vuông góc với mặt phẳng đáy.
Tính chất
Suy ra: 
Các bước xác định trục
Bước 1:Xác định tâm của đường tròn ngoại tiếp đa giác đáy.
Bước 2:Qua dựng vuông góc với mặt phẳng đáy.
Một số trường hợp đặc biệt
Đáy là tam giác vuông
Đáy là tam giác đều
Đáy là tam giác thường
5.3.2. Kỹ năng tam giác đồng dạng
Nội dung
Hình vẽ
 đồng dạng với .
5.3.3. Nhận xét quan trọng
 là trục đường tròn ngoại tiếp .
5.4. Kỹ thuật sử dụng hai trục xác định tâm mặt cầu ngoại tiếp đa diện
Nội dung
Hình vẽ
Cho hình chóp (thõa mãn điều kiện tồn tại mặt cầu ngoại tiếp). Thông thường, để xác định mặt cầu ngoại tiếp hình chóp ta thực hiện theo hai bước:
Bước 1:
Xác định tâm của đường tròn ngoại tiếp đa giác đáy. Dựng : trục đường tròn ngoại tiếp đa giác đáy.
Bước 2:
Xác định trục của đường tròn ngoại tiếp một mặt bên (dễ xác định) của khối chóp. 
Lúc đó: 
Tâm của mặt cầu: 
Bk: . Tuỳ vào từng trường hợp.
5.5. Tổng kết các dạng tìm tâm và bán kính mặt cầu
5.5.1. Dạng 1
Nội dung
Hình vẽ
Cạnh bên vuông góc đáy và khi đó và tâm là trung điểm .
5.5.2. Dạng 2
Nội dung
Hình vẽ
Cạnh bên vuông góc đáy và bất kể đáy là hình gì, chỉ cần tìm được bán kính đường tròn ngoại tiếp của đáy là , khi đó :
(: nửa chu vi).
Nếu vuông tại thì: .
Đáy là hình vuông cạnh thì 
 nếu đáy là tam giác đều cạnh thì .
5.5.3. Dạng 3
Nội dung
Hình vẽ
Chóp có các cạnh bên bằng nhau: :
.
 là hình vuông, hình chữ nhật, khi đó là giao hai đường chéo.
 vuông, khi đó là trung điểm cạnh huyền.
 đều, khi đó là trọng tâm, trực tâm.
5.5.4. Dạng 4
Nội dung
Hình vẽ
Hai mặt phẳng và vuông góc với nhau và có giao tuyến . Khi đó ta gọi lần lượt là bán kính đường tròn ngoại tiếp các tam giác và . Bán kính mặt cầu ngoại tiếp: 
5.5.5. Dạng 5
Chóp có đường cao , tâm đường tròn ngoại tiếp đáy là . Khi đó ta giải phương trình: . Với giá trị tìm được ta có: .
5.5.6. Dạng 6: Bán kính mặt cầu nội tiếp: .
6. TỔNG HỢP CÁC CÔNG THỨC ĐẶC BIỆT VỀ KHỐI TRÒN XOAY
6.1. Chỏm cầu
Nội dung
Hình vẽ
6.2. Hình trụ cụt
Nội dung
Hình vẽ
6.3. Hình nêm loại 1
Nội dung
Hình vẽ
6.4. Hình nêm loại 2
Nội dung
Hình vẽ
6.5. Parabol bậc hai-Paraboloid tròn xoay
Nội dung
Hình vẽ
6.6. Diện tích Elip và Thể tích khối tròn xoay sinh bởi Elip
Nội dung
Hình vẽ
6.7. Diện tích hình vành khăn
Nội dung
Hình vẽ
6.8. Thể tích hình xuyến (phao)
Nội dung
Hình vẽ
II. BÀI TẬP TRẮC NGHIỆM
MẶT TRÒN XOAY – KHỐI TRÒN XOAY
Câu 1:	thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục 
A. .	B. .	C. .	D. .
Hướng dẫn giải:
Chọn A. 
Ta có 
Khi quay quanh trục, tam giác tạo ra một hình nón có thể tích
Khi quay quanh trục, hình vuông tạo ra một hình trụ có thể tích
Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục là
Câu 2:	Thể tích của khối tròn xoay thu được khi quay hình thang quanh trục , biết . 
A. 	B. 	C. 	D. 
	Hướng dẫn giải:
Chọn C. 
Công thức tính thể tích khối nón cụt .
Trong đó là độ dài đường cao, lần lượt là bán kính hai đáy.
Gọi là thể tích khối nón cụt khi quay hình thang quanh trục .
Gọi là thể tích khối nón cụt khi quay hình thang quanh trục .
Khi đó .	
Ta có 
và.
Vậy .
Câu 3:	Cho đoạn thẳng AB có độ dài bằng ,vẽ tia về phía điểm B sao cho điểm B luôn cách tia một đoạn bằng . Gọi H là hình chiếu của B lên tia, khi tam giác AHB quay quanh trục AB thì đường gấp khúc AHB vẽ thành mặt tròn xoay có diện tích xung quanh bằng
A.	B. 	C. 	D. 
Hướng dẫn giải:
Chọn B. 
Khi quay quanh tam giác AHB thì đường gấp khúc AHB vẽ lên một mặt tròn xoay. Diện tích mặt tròn xoay này bằng tổng diện tích xung quanh hai hình nón đường sinh AH và BH.
Ta có 
Diện tích xung quanh hình nón có đường sinh AH là 
Diện tích xung quanh hình nón có đường sinh BH là 
Diện tích mặt tròn xoay cần tìm là .
Câu 4:	Cho ba hình tam giác đều cạnh bằng chồng lên nhau như hình vẽ (cạnh đáy của tam giác trên đi qua các trung điểm hai cạnh bên của tam gác dưới). Tính theo thể tích của khối tròn xoay tạo thành khi quay chúng xung quanh đường thẳng .
A. .	B. .
C. .	D. .
Chọn B. 
Nếu ba hình tam giác không chồng lên nhau thì
thể tích của khối tròn xoay là 
Thể tích phần bị chồng lên là 
Þ Thể tích cần tính là 
Hoặc làm như sau:
Đặt lần lượt là thể tích: khối nón sinh bởi tam giácquay quanh , khối tròn xoay sinh bởi hình , khối nón sinh bởi tam giác khi quay quanh . Khi đó: Thể tích khối cần tìm là:
Câu 5:	Cho nửa đường tròn đường kính và điểm thay đổi trên nửa đường tròn đó, đặt và gọi là hình chiếu vuông góc của lên . Tìm sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác quanh trục đạt giá trị lớn nhất.
A. .	B. .	C. .	D. .
Hướng dẫn giải:
Thể tích vật thể tròn xoay tạo thành khi quay tam giác quanh trục là
.
Đặt 
Vậy lớn nhất khi khi .
@Chú ý: có thể dùng PP hàm số để tìm GTNN của hàm 
Chọn C. 
Câu 6:	Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một nón tròn xoay (N) có góc ở đỉnh bằng . Tính tỉ số thể tích của hình trụ (T) và hình nón (N).
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Bài toán quy về hình nón tâm O ngoại tiếp hình vuông ABCD và nội tiếp tam giác đều SEF mà Vì OAB là tam giác vuông cân nên .Suy ra 
Ta thấy, tâm O của hình tròn cũng chính là tâm của hình vuông ABCD đồng thời cũng là trọng tâm của tam giác đều SEF. Như vậy, đường cao của tam giác SEF là 
Trong tam giác EOH (vuông tại H, ). Ta có: 
Thể tích của hình nón 
Vậy .
Chọn A. 
Câu 7:	Cho tam giác đều và hình vuông cùng có cạnh bằng được xếp chồng lên nhau sao cho một đỉnh của tam giác đều trùng với tâm của hình vuông, trục của tam giác đều trùng với trục của hình vuông (như hình vẽ). Thể tích của vật thể tròn xoay sinh bởi hình đã cho khi quay quanh trục là
A. 	B. C. 	D. 
Hướng dẫn giải:
Chọn D.
Khi xoay quanh trục AB thì:
· Phần hình vuông phía trên trở thành lăng trụ có bán kính R = 2, chiều cao h = 4
Phần dưới trở thành hình nón cụt với
;
Áp dụng 
Vậy .
Câu 8:	Cho hai hình vuông có cùng cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh của một hình vuông là tâm của hình vuông còn lại (như hình vẽ). Tính thể tích của vật thể tròn xoay khi quay mô hình trên xung quanh trục .
A. . B. . C. .	D. .
Hướng dẫn giải:
Chọn C. 
· Cách 1 :
Khối tròn xoay gồm 3 phần:
Phần 1: khối trụ có chiều cao bằng 5, bán kính đáy bằng có thể tích .
Phần 2: khối nón có chiều cao và bán kính đáy bằng có thể tích
Phần 3: khối nón cụt có thể tích là
.
Vậy thể tích khối tròn xoay là
.
· Cách 2 :
Thể tích hình trụ được tạo thành từ hình vuông là
Thể tích khối tròn xoay được tạo thành từ hình vuông là
Thể tích khối tròn xoay được tạo thành từ tam giác là
Thể tích cần tìm .
Câu 9:	Cho tam giác đều cạnh và nội tiếp trong đường tròn tâm , là đường kính của đường tròn tâm . Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm (hình vẽ bên) quay quanh đường thẳng bằng
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Chọn A. 
Khi quay tam giác quanh trục được khối nón có thể tích là:
Khi quay đường tròn tâm quanh trục được khối cầu có thể tích là:
Thể tích khối tròn xoay cần tìm: 
Câu 10:	Cho hình thang vuông có độ dài hai đáy , đường cao . Quay hình thang quanh đường thẳng thu được khối tròn xoay . Tính thể tích của khối .
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Chọn D. 
Gọi là thể tích khối trụ khi quay hình chữ nhật quanh trục 
Gọi là thể tích khối nón. Khi quay quanh trục 
là thể tích của khối cần tìm
=
Câu 11:	Cho tam giác vuông tại có . Khi tam giác quay quanh đường thẳng ta được một khối tròn xoay. Tính thể tích của khối tròn xoay đó.
A. .	B. .	C. .	D. .
Hướng dẫn giải:
Chọn A. 
Gọi là hình chiếu vuông góc của lên Gọi lần lượt là thể tích khối nón do tam giác và sinh ra khi quay quanh trục 
Ta có: .
Suy ra 
Vậy 
Câu 12:	Cho hình phẳng được mô tả ở hình vẽ dưới đây. Tính thể tích của vật thể tròn xoay được tạo ra khi quay hình phẳng quanh cạnh .
A
7
cm
6
cm
3
cm
3
cm
5
cm
B
C
E
F
D
A.	B.	C.	D.
Hướng dẫn giải: Chọn A.
Vật thể tròn xoay tạo ra gồm hai phần:
 là phần hình trụ tròn xoay quay bởi hình gấp khúc quanh trục tạo ra hình trụ có chiều cao bán kính đáy 
 là phần hình trụ tròn xoay quay bởi hình gấp khúc quanh trục tạo ra hình nón cụt có chiều cao bán kính đáy lớn bán kính đáy bé 
Khi đó thể tích khối tròn xoay là:
.
MẶT NÓN – KHỐI NÓN
Câu 1:	Hình nón tròn xoay nội tiếp trong tứ diện đều cạnh bằng a có diện tích xung quanh bằng:
A.	B.	C.	D.
Hướng dẫn giải:
Gọi là tứ diện đều cạnh
Gọi H là trung điểm cạnh 
Kẻ thì 
là đường sinh của hình nón.
Ba điểm thẳng hàng.
Chọn A.
Câu 2:	Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh bằng a có diện tích xung quanh bằng:
A.	B.	C.	D.
Hướng dẫn giải:
Kẻ 
Ta có: 
Chọn C.
Câu 3:	Một bình đựng nước dạng hình nón (không đáy) đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó. Người ta thả vào đó một khối trụ và đo dược thể tích nước tràn ra ngoài là . Biết rằng một mặt của khối trụ nằm trên mặt trên của hình nón, các điểm trên đường tròn đáy còn lại đều thuộc các đường sinh của hình nón (như hình vẽ) và khối trụ có chiều cao bằng đường kính đáy của hình nón. Diện tích xung quanh của bình nước là:
A..	B..	C..	D..
Hướng dẫn giải:
Chọn B.
Xét hình nón: , . Xét hình trụ: , 
 Thể tích khối trụ là: 
Câu 4:	Cho khối nón tròn xoay có đường cao , bán kính đáy . Một mặt phẳng (P) đi qua 2 đỉnh của khối nón và có khoảng cách đến tâm O của đáy là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng:
A.	B.	C.	D.
Hướng dẫn giải:
Gọi S là đỉnh của khối nón. Mặt phẳng (P) đi qua đỉnh S cắt khối nón theo hai đường sinh bằng nhau là nên ta có thiết diện là tam giác cân 
Gọi I là trung điểm của đoạn AB, ta có . Từ tâm O của đáy ta kẻ tại H, ta có và do đó theo giả thiết ta có . Xét tam giác vuông SOI ta có:
Mặt khác, xét tam giác vuông SOI ta còn có: 
Do đó 
Gọi St là diện tích của thiết diện Ta có: , trong đó 
Vì nên và 
Vậy thiết diện SAB có diện tích là: .
Chọn A.
Câu 5:	Cho tam giác ABC có độ dài cạnh huyền 5. Người ta quay tam giác ABC quanh một cạnh góc vuông để sinh ra hình nón. Hỏi thể tích V khối nón sinh ra lớn nhất là bao nhiêu.
A.	B.	C.	D.
Hướng dẫn giải:
Ta có .
Xét hàm số với .
Ta có .
Khi đó thể tích lớn nhất là .
Chọn A.
Câu 6:	Cho hình thang cân có đáy nhỏ , đáy lớn , cạnh bên quay quanh đường thẳng . Tính thể tích của khối tròn xoay tạo thành.
A..	B..	C..	D..
Hướng dẫn giải:
Chọn C.
Theo hình vẽ: .
Thể tích khối tròn xoay tạo thành bằng thể
tích khối trụ có bán kính , chiều
cao trừ đi thể tích hai khối nón bằng
nhau (khối nón đỉnh A, đỉnh B và đáy là đáy của hình trụ).
Vậy .
Câu 7:	Cho hình bình hành có và Quay quanh AB, ta được vật tròn xoay có thể tích là:
A.	B.
C.	D.
Hướng dẫn giải:
Kẻ 
Các tam giác vuông HAD và NBC
bằng nhau.
Khi quay quanh AB, các tam giác vuông
 và tạo thành hai hình nón tròn xoay bằng nhau nên:
Chọn C.
Câu 8:	Cho khối nón đỉnh , trục . Măt phẳng trung trực của chia khối chóp thành hai phần. Tỉ số thể tích của hai phần là:
A..	B..	C..	D..
Hướng dẫn giải:
Chọn D.
Gọi là bán kính đáy của khối nón trục .
Giả sử mặt phẳng trung trực của cắt trục tại , cắt đường sinh tại . Khi đó mặt phẳng này chia khối nón thành 2 phần, phần trên là khối nón mới có bán kính , có chiều cao là . Phần dưới là khối nón cụt có thể tích .
Vậy tỉ số thể tích là: 	
Câu 9:	Cho hình nón có bán kính đáy R, đường cao SO. Gọi (P) mà mặt phẳng vuông góc với SO tại O1 sao cho . Một mặt phẳng qua trục hình nón cắt phần khối nón nằm giữa (P) và đáy hình nón theo thiết diện là hình tứ giác có hai đường chéo vuông góc. Tính thể tích phần hình nón nằm giữa mặt phẳng (P) và mặt phẳng chứa đáy hình nón .
A.	B.	C.	D.
Hướng dẫn giải:
Gọi thiết diện thu được là 
Vì nên 
Mặt khác tại I nên
Vậy 
Dễ thấy 
Từ đó 
Gọi thể tích phần hình nón phải tính là V* thì , trong đó:
V1 là thể tích của hình nón .
V2 là thể tích hình nón đỉnh S và đáy là thiết diện của được cắt bởi (P).
Ta có thể tích phần hình nón phải tính là
Câu 10:	Hình nón tròn xoay có trục với R là bán kính đáy, thiết diện qua trục của hình nón tạo thành tam giác SAB là tam giác đều. Gọi I là trung điểm của SO và E, F sao cho Khi đó, tâm mặt cầu ngoại tiếp hình nón là điểm:
A.	B.	C.	D.
Hướng dẫn giải:
Gọi là tâm mặt cầu ngoại tiếp hình nón thì:
Ta có: 
Vậy 
Chọn B.
Câu 11:	Cho hình nón tròn xoay đỉnh S, đáy là đường tròn tâm O, bán kính Một thiết diện qua đỉnh S tạo thành tam giác SAB sao cho tam giác SAB đều, cạnh bằng 8. Khoảng cách từ O đến thiết diện là:
A.	B.	C.	D.
Hướng dẫn giải:
 kẻ 
Kẻ thì nên 
Chọn B.
Câu 12:	Cho một hình nón có bán kính đáy là , chiều cao là , ngoại tiếp một hình cầu . Khi đó, thể tích của khối trụ ngoại tiếp hình cầu là
A..	B..	C..	D..
 Hướng dẫn giải:
Giả sử hình nón có đỉnh và đường kính đáy là .
Ta có .
Tam giác có diện tích là ,
chu vi là .
Do đó bán kính khối cầu là .
Thể tích khối trụ cần tìm là: .
Câu 13:	Một hình nón bị cắt bởi mặt phẳng song song với đáy. Mặt phẳng chia hình nón làm hai phần và . Cho hình cầu nội tiếp như hình vẽ sao cho thể tích hình cầu bằng một nửa thể tích của . Một mặt phẳng đi qua trục hình nón và vuông góc với đáy cắt theo thiết diện là hình thang cân, tang góc nhọn của hình thang cân là
A.	B.	C.	D.
Hướng dẫn giải:
Giả sử ta có mặt cắt của hình nón cụt và các đại lượng như hình vẽ.
Gọi là góc cần tìm.
Xét vuông tại có 
Thể tích khối cầu là 
Thể tích của là 
Ta có (tính chất hai tiếp tuyến cắt nhau)
Mà 
Từ 
Từ (vì là góc nhọn)
Chọn A.
Câu 14:	Trong các hình nón nội tiếp một hình cầu có bán kính bằng 3, tính bán kính mặt đáy của hình nón có thể tích lớn nhất.
A..	B.	C.	D.
Hướng dẫn giải:
Chọn D.
Giả sử chóp đỉnh như hình vẽ là hình chóp có thể tích lớn nhất.
 vuông tại Ta thấy là bán kính đáy của chóp, là chiều cao của chóp.
 trên
Câu 15:	Trong tất cả các hình nón có độ dài đường sinh bằng , tìm hình nón có thể tích lớn nhất
A..	B..	C..	D..
Hướng dẫn giải:
Chọn A.
Gọi là chiều cao của nón thì bán kính nón là . Suy ra:
, với 
Xét hàm số trong ta thấy hay .
Câu 16:	Trong các hình nón tròn xoay cùng có diện tích toàn phần bằng . Tính thể tích hình nón lớn nhất?
A..	B..	C..	D..
Hướng dẫn giải:
Chọn B.
Ta có suy ra và .
Có .
Xét hàm số trên đoạn ta có tại .
Vậy .
Câu 17:	Giá trị lớn nhất của thể tích khối nón nội tiếp trong khối cầu có bán kính là
A..	B..	C..	D..
Hướng dẫn giải:
Rõ ràng trong hai khối nón cùng bán kính đáy nội tiếp trong một khối cầu thì khối nón có chiều cao lớn hơn thì thể tích lớn hơn, nên ta chỉ xét khối nón có chiều cao lớn hơn trong hai khối nón đó.
Giả sử rằng khối nón có đáy là hình tròn bán kính . Gọi với là khoảng cách giữa tâm khối cầu đến đáy khối nón. Khi đó chiều cao lớn nhất của khối nón nội tiếp khối cầu với đáy là hình tròn sẽ là . Khi đó bán kính đáy nón là , suy ra thể tích khối nón là
Áp dụng BĐT Cô-si ta có 
Chọn D.
Câu 18:	Tìm hình nón có thể tích nhỏ nhất ngoại tiếp mặt cầu bán kính cho trước có thể tích bằng:
A.	B.	C.	D.
Hướng dẫn giải:
Xét mặt phẳng chứa trục của hình nón, mặt phẳng này cắt hình nón theo tam giác cân và cắt mặt cầu nội tiếp hình nón theo đường tròn bán kính và hình tròn này nội tiếp tam giác cân 
Kí hiệu bán kính đáy hình nón là , chiều cao hình nón là thì 
\
Vậy thể tích hình nón ngoại tiếp mặt cầu bán kính là
Ta có 
Từ đó , tức là đạt giá trị bé nhất khi và chỉ khi từ đó .
Câu 19:	Cho một hình nón có đáy là hình tròn tâm. Đường kính và đường cao . Cho điểm thay đổi trên đoạn thẳng. Mặt phẳng vuông góc với tạivà cắt hình nón theo đường tròn . Khối nón có đỉnh là và đáy là hình tròn có thể tích lớn nhất bằng bao nhiêu?
A.	B.	C.	D.
Hướng dẫn giải:
Gọi là mặt phẳng qua trục của hình nón cắt hình nón theo thiết là tam giác SAB, cắt hình nón đỉnh S và có đáy là đường tròn theo thiết diện là tam giác SCD, gọi I là giao điểm của SO và . Ta có: .Do đó tam giác vuông cân tại .Suy ra tam giác vuông cân tại .Đặt 
Thể tích khối nón có đỉnh là và đáy là hình tròn là:
.
Bảng biến thiên:
Chọn B.
Câu 20:	Cho hình nón có chiều cao . Tính chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo .
A..	B..	C..	D..
Hướng dẫn giải:
Gọi theo thứ tự là bán kính đáy hình nón và khối trụ cần tìm. là đỉnh của hình nón, là tâm của đáy hình nón, là tâm của đáy hình trụ và khác . là một đường sinh của hình nón, là điểm chung của với khối trụ. Ta có: .
Thể tích khối trụ là: 
Xét hàm số .
Ta có
Bảng biến thiên:
Dựa vào BBT, ta thấy thể tích khối trụ lớn nhất khi chiều cao của khối trụ là ;.
MẶT TRỤ - KHỐI TRỤ
Câu 1:	Một hình trụ có bán kính đáy R và có thiết diện qua trục là một hình vuông. Tính thể tích của khối lăng trụ tứ giác đều nội tiếp trong khối trụ đã cho.
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Giả sử là khối lăng trụ
tứ giác đều nội tiếp hình trụ đã cho.
Từ giả thiết, suy ra hình trụ có chiều cao
 và đáy là hình vuông
nội tiếp đường tròn bán kính 
Do đó 
Diện tích hình vuông là:
Vậy thể tích của khối lăng trụ đã cho là:
Chọn A. 
Câu 2:	Một khối lăng trụ tam giác đều cạnh đáy bằng góc giữa đường chéo mỗi mặt bên và mặt đáy bằng Tính thể tích khối trụ ngoại tiếp khối lăng trụ đó.
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Xét hình lăng trụ tam giác đều
 có cạnh đáy 
góc của đường chéo A’B với mặt
đáy là 
Suy ra: 
Khối trụ ngoại tiếp khối lăng trụ có cùng
đường cao là A’A, đáy là đường tròn
ngoại tiếp hai mặt đáy ,
có bán kính R cho bởi 
Thể tích khối trụ:
 (đvdt).
Chọn A. 
Câu 3:	Một khối lăng trụ tam giác đều có cạnh đáy bằng và chiều cao bằng nội tiếp một khối trụ. Tính thể tích khối trụ đó.
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Hình trụ có đáy là đường tròn ngoại
tiếp tam giác 
Do ABC là tam giác đều cạnh a nên
hình trụ có bán kính là:
với 
Chiều cao của hình trụ bằng chiều cao
của lăng trụ là 
Vậy thể tích khối trụ là:
Chọn A. 
Câu 4:	Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng Trên đường tròn đáy tâm O lấy điểm A, trên đường đáy tâm O’ lấy điểm B sao cho Tính thể tích của khối tứ diện 
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Kẻ đường sinh AA’. Gọi D là điểm đối xúng của A’ qua O’ và H là hình chiếu vuông góc của B trên đường thẳng 
Do đó, BH là chiều cao của tứ diện 
Thể tích khối tứ diện 
Tam giác vuông tại A’ cho: 
Tam giác 
Suy ra là tam giác đều cạnh 
Từ đó 
Do nên tam giác 
vuông cân tại O.
Diện tích tam giác là:
. Vậy 
Chọn A. 
Câu 5:	Một hình trụ có thiết diện qua trục là hình vuông. Bên trong hình trụ có một hình lăng trụ tứ giác đều nội tiếp. Nếu thể tích hình lăng trụ là V thì thể tích hình trụ bằng bao nhiêu?
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Gọi cạnh đáy lăng trụ là 
Thiết diện qua hình trụ là hình vuông.
Thể tích lăng trụ bằng V
Thể tích hình trụ tính theo 
Thay .
Chọn A. 
Câu 6:	Cho hình nón có độ dài đường kính đáy là , độ dài đường sinh là và hình trụ có chiều cao và đường kính đáy đều bằng , lồng vào nhau như hình vẽ.
Tính thể tích phần khối trụ không giao với khối nón
A. .	B. .	C. .	D. .
Hướng dẫn giải:
Chọn D. 
Ta có .
Thể tích khối nón lớn (có đường cao ) là .
Thể tích khối nón nhỏ (có đường cao ) là 
Thể tích phần khối giao nhau giữ khối nón và khối trụ là .
Thể tích khối trụ là là .
Vậy thể tích phần khối trụ không giao với khối nón là .
Câu 7:	Cắt một khối trụ bởi một mặt phẳng ta được một khối như hình vẽ bên. Biết rằng thiết diện là một hình elip có độ dài trục lớn bằng 8, khoảng cách từ điểm thuộc thiết diện gần mặt đáy nhất và điểm thuộc thiết diện xa mặt đáy nhất tới mặt đáy lần lượt là 8 và 14 (xem hình vẽ).Tính thể tích của .
A. .
B. .
C. .
D. .
Hướng dẫn giải:
Chọn D. 
Đường kính đáy của khối trụ là 
Bán kính đáy của khối trụ là 
Thể tích của khối trụ là .
Thể tích của khối trụ là .
Thể tích của H là .
Câu 8:	Cắt một khối trụ bởi một mặt phẳng ta được một khối như hình vẽ. biết rằng thiết diện là một elip có độ dài trục lớn là , khoảng cách từ điểm thuộc thiết diện gần mặt đáy nhất và điểm thuộc thiết diện xa mặt đáy nhất tới mặt đáy lần lượt là và . Tính thể tích của 
A. 	B. 
C. 	D. 
Hướng dẫn giải:
Dùng một mặt phẳng đi qua N và vuông góc với trục của hình cắt hình thành 2 phần có thể tích lần lượt là 
Ta có 
Phần phía trên có thể tích bằng một nửa của hình trụ có 
Vậy 
Câu 9:	Cho hình lập phương Gọi O’, O là tâm của hai hình vuông ABCD và và Gọi là thể tích của hình trụ tròn xoay đáy là hai đường tròn ngoại tiếp các hình vuông và là thể tích hình nón tròn xoay đỉnh O’ và đáy là đường tròn nội tiếp hình vuông Tỉ số thể tích là:
A. 	B. 3	C. 4	D. 6
Hướng dẫn giải:
Gọi M trung điểm của AB thì tam
giác OAM vuông cân tại M.
Chọn D. 
Câu 10:	Cho lăng trụ đáy là tam giác có và góc Gọi lần lượt là thể tích của khối lăng trụ ngoại tiếp và nội tiếp khối lăng trụ đã cho. Tính tỉ số 
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Áp dụng đinh lý cosin trong tam giác ABC ta c
Diện tích tam giác ABC là: 
Mặt khác:
 với R là bán kính đường tròn ngoại tiếp tam giác 
Ngoài ra: trong đó và là bán kính đường tròn nội tiếp tam giác ABC 
Hình trụ ngoại tiếp và nội tiếp lăng trụ đã cho có bán kính đáy lần lượt là và có chiều cao bằng chiều cao của hình lăng trụ.
Giả sử là chiều cao hình lăng trụ, ta có: và 
Vậy 
Chọn A. 
Câu 11:	Cho một khối trụ có bán kính đáy và chiều cao . Mặt phẳng song song với trục của khối trụ chia khối trụ thành 2 phần, gọi là thể tích phần khối trụ chứa trục , là thể tích phần còn lại của khối trụ. Tính tỉ số , biết rằng cách một khoảng bằng .
A. .	B. .	C. .	D. .
Hướng dẫn giải:
Thể tích khối trụ .
Gọi thiết diện là hình chữ nhật .
Dựng lăng trụ như hình vẽ.
Gọi H là trung điểm 
Ta có Þ
Þ.
ÞDOAB vuông cân tại O Þ ABCD là hình vuông.
Từ đó suy ra:
.
. Suy ra .
Chọn A. 
Câu 12:	Cho một hình trụ có bán kính đáy chiều cao Một đoạn thẳng có độ dài bằng 10 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách giữa đường thẳng và trục của hình trụ?
A. 	B. 	
C. 	D. 
Hướng dẫn giải:
Gọi hai đường tròn đáy là và
 Kẻ hai đường sinh
 ta được tứ giác là một
hình chữ nhật và 
Do đó, khoảng cách giữa OO’ và AB
bằng khoảng cách từ O đến 
Tam giác ACB vuông tại C nên ta có:
Gọi I là trung điểm AC, ta có:
Vậy khoảng cách giữa đường thẳng AB và trục OO’ của hình trụ là: 
Chọn B. 
Câu 13:	Một hình trụ có bán kính đáy bằng 50cm và có chiều cao là 50cm. Một đoạn thẳng AB có chiều dài là 100cm và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng đó đến trục hình trụ.
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Kẻ AA1 vuông góc với đáy, A1 thuộc đáy. Suy ra:
Tiếp tục kẻ tại H, vì O1H nằm trong đáy nên cũng vuông góc với A1A suy ra:
. Do đó 
Xét tam giác vuông ta có 
Vậy 
Chọn C. 
Câu 14:	Cho hình trụ có bán kính đáy R và chiều cao R lấy hai điểm A, B nằm trên hai đường tròn đáy sao cho Tính khoảng cách từ AB đến hình trụ theo R.
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Giả sử đường tròn O, 
Từ A vẽ đường song song OO’ cắt
đường tròn tại A’.
Vẽ O’H vuông góc 
Từ H vẽ đường thẳng song song với OO’,
cắt AB tại K. Vẽ 
Ta có: và nên:
 và 
Vậy tứ giác là hình chữ
nhật 
Vậy KI là đoạn vuông góc chung của
AB và vuông
Do H trung điểm A’B nên: 
Do đó: 
Chọn A. 
Câu 15:	Cho là thiết diện song song với trục OO’ của hình trụ (A, B thuộc đường tròn tâm O). Cho biết và thể tích của hình trụ bằng Khoảng cách d từ O đến mặt phẳng là:
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Kẻ thì 
Và 
Ta có 
Mà 
Chọn B. 
Câu 16:	Cho hình trụ có hai đáy là hai đường tròn và , chiều cao bằng và bán kính đáy . Một mặt phẳng đi qua trung điểm của và tạo với một góc , cắt đường tròn đáy theo một dây cung. Tính độ dài dây cung đó theo .
A. .	B. .	C. .	D. .
Hướng dẫn giải:
Chọn B. 
Dựng 
 là hình chiếu của lên 
Theo bài ta được 
Xét tam giác vuông vuông tại 
Xét tam giác vuông tại 
Câu 17:	Cho một hình trụ có bán kính đáy bằng và có chiều cao bằng Hai điểm lần lượt nằm trên hai đường tròn đáy sao cho góc giữa và trục của hình trụ bằng . Khoảng cách giữa và trục của hình trụ bằng:
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Từ hình vẽ kết hợp với giả thiết, ta có 
Gọi là đường sinh của hình trụ thì
 và .
Vì nên
Gọi là trung điểm , suy ra
 nên .
Tam giác vuông tại nên 
Suy ra tam giác đều có cạnh bằng nên 
Chọn C. 
Câu 18:	Cho mặt cầu bán kính . Một hình trụ có chiều cao và bán kính đáy thay đổi nội tiếp mặt cầu. Tính chiều cao theo bán kính sao cho diện tích xung quanh hình trụ lớn nhất
A. .	B. .	C. .	D. .
Hướng dẫn giải:
Chọn A. 
Ta có .
Diện tích xung quanh của hình trụ
,
(dùng BĐT ).
Vậy .
Câu 19:	Cho hình trụ có chiều caobán kính đáyMột mặt phẳng không vuông góc với đáy của hình trụ, làn lượt cắt hai đáy theo đoạn giao tuyến và sao cho là hình vuông. Tính diện tích của hình vuông.
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Kẻ đường sinh BB’ của hình trụ. Đặt độ dài cạnh của hình vuông ABCD là x, x > 0.
Do vuông tại	C. Khi đó, B’D là đường kính của đường
Tròn . Xét vuông tại C
Xét tam giác vuông tại B
Từ (1) và (2) .
Suy ra diện tích hình vuông ABCD là .
Câu 20:	Một hình trụ có thể tích V không đổi. Tính mối quan hệ giữa bán kính đáy và chiều cao hình trụ sao cho diện tích toàn phần đạt giá trị nhỏ nhất.
A. 	B. 	C. 	D. 
Hướng dẫn giải:
Gọi R và là bán kính đáy và chiều cao hình trụ.
Ta có: (không đổi)
Áp dụng bất đẳng thức Cauchy cho 3 số dương,
Ta có: 
(hằng số)
Do đó: S toàn phần đạt giá trị nhỏ nhất
Chọn A. 
MẶT CẦU – KHỐI CẦU
Câu 1:	Cho hình chóp có , , và Gọi , lần lượt là hình chiếu của trên , . Tính bán kính của mặt cầu đi qua các điểm , , , , .
A..	B..	C..	D..
Hướng dẫn giải:
Chọn D.
*Gọi là trung điểm của suy ra :
*Lại có 
*Theo giả thiêt 
* Chứng minh 
Thật vậy, ta có:
Từ suy ra các điểm , , , , nội tiếp đường tròn tâm , bán kính .
Câu 2:	Cho hình chóp S.ABCD, đáy ABCD là hình vuông, cạnh 2a, tâm O, mặt bên (SAB) là tam giác đều và . Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp đó.
A.	B.	C.	D.
Hướng dẫn giải:
Qua O, kẻ thì là trục của đường tròn ngoại tiếp hình vuông 
Do nên kẻ thì 
Gọi E là tâm đường tròn ngoại tiếp tam giác đều SAB và kẻ tại E thì là trục của đường tròn ngoại tiếp tam giác 
cắt tại I: tâm của mặt cầu ngoại tiếp hình chóp 
Tứ giác OHEI có 3 góc vuông O, H, E nên là hình chữ nhật
Trong .
Chọn A.
Câu 3:	Cho hình chóp có đáy là tam giác đều cạnh , hình chiếu vuông góc của đỉnh trên mặt phẳng là trung điểm của cạnh . Góc giữa đường thẳng và mặt phẳng bằng . Gọi là trọng tâm tam giác , là bán kính mặt cầu có tâm và tiếp xúc với mặt phẳng . Đẳng thức nào sau đây sai?
A.	B.	C.	D.
Hướng dẫn giải:
Ta có .
Tam giác đều cạnh nên .
Trong tam giác vuông , ta có .
Vì mặt cầu có tâm và tiếp xúc với nên bán kính mặt cầu 
Ta có 
Gọi lần lượt là trung điểm và .
Suy ra và .
Gọi là hình chiếu vuông góc của trên , suy ra . 
Ta có 
Từ và , suy ra nên .
Trong tam giác vuông , ta có .
Vậy .
Chọn D.
Câu 4:	Cho lăng trụ đứng có đáy là tam giác đều cạnh . Mặt phẳng tạo với mặt đáy góc và điểm là trọng tâm tam giác . Bán kính mặt cầu ngoại tiếp khối chóp bằng:
A.	B..	C.	D.
Hướng dẫn giải: Chọn D.
Gọi là trung điểm , ta có .
Trong , có ; .
Gọi là trọng tâm tam giác đều , suy ra cũng là tâm đường tròn ngoại tiếp 
Vì lặng trụ đứng nên .
Do đó là trục của tam giác .
Trong mặt phẳng , kẻ trung trực của đoạn thẳng cắt tại . Khi đó là tâm mặt cầu ngoại tiếp khối chóp , bán kính 
Ta có 
Câu 5:	Cho hình chóp đều có đường cao ; góc bằng 45 độ. Bán kính mặt cầu ngoại tiếp hình chóp là
A.	B.	C.	D.
Hướng dẫn giải: Gọi I là tâm của mặt cầu ngoại tiếp hình chop S.ABCD
Khi đó hay 
Gọi H là giao điểm của AC và Từ (1) suy ra 
Trong mặt phẳng (SAH) dựng đường thẳng là trung trực của 
Từ (2), suy ra 
Gọi M là trung điểm của SA, khi đó:
. Do SAB cân tại S và có nên SAB vuông cân tại S. Đặt , khi đó 
Trong tam giác vuông SHA có:
Chọn C.
Câu 6:	Cho khối chópcó ; đáy là hình thang vuông tại và với; . Gọi là trung điểm của . Tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp .
A.	B.	C.	D.
Hướng dẫn giải:
Gọi là trung điểm của .
Kẻ tia thì .
Ta có: là tâm đường tròn ngoại tiếp tam giác vuông và , nên là trục của đường tròn .
Gọi lần lượt là trung điểm của .
Ta có: ; nên suy ra .
Do đó tam giác cân tại , suy ra .
Dễ thấy và nên suy ra và do đó .
Vậy nên , do đó là trục của đường tròn .
Gọi là giao điểm của và thì chính là tâm mặt cầu ngoại tiếp hình chóp .
Bán kính mặt cầu ngoại tiếp hình chóp là .
Trong đó và ( là giao điểm của và ).
Vậy thì .
Chọn C.
Câu 7:	Cho hình chóp tam giác đều có cạnh đáy bằng và cạnh bên bằng . Gọi là chiều cao của khối chóp và là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số bằng:
A.	B.	C.	D.
Hướng dẫn giải:
Gọi là tâm , suy ra và 
Trong , ta có 
Trong mặt phẳng , kẻ trung trực của đoạn 
cắt tại , suy ra
● nên .
● nên .
Do đó nên là tâm mặt cầu ngoại tiếp khối chóp .
Gọi là tung điểm , ta có nên
 Vậy 
Chọn C.
Câu 8:	Cho hình chóp có đáy ABCD là hình thang cân, đáy lớn 
Cạnh bên và vuông góc với đáy. Gọi R bán kính mặt cầu ngoại tiếp khối chóp . Tỉ số nhận giá trị nào sau đây?
A.	B.	C.	D.
Hướng dẫn giải:
Ta có hay 
Gọi là trung điểm 
Ta có Nên ABCE là
hình thoi. Suy ra 
Do đó tam giác vuông tại	C.
Ta có:
hay 
Tương tự, ta cũng có hay 
Ta có nên khối chóp nhận trung điểm I của SD làm tâm mặt cầu ngoại tiếp, bán kính 
Suy ra 
Chọn D.
Câu 9:	Cho hình chóp có đáy ABCD là hình chữ nhật với Cạnh bên SA vuông góc với đáy và góc giữa SC với đáy bằng Gọi N là trung điểm SA, h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp Biểu thức liên hệ giữa R và là:
A.	B.	C.	D.
Hướng dẫn giải:
Ta có 
Trong ta có 
Ta có 
Lại có Do đó, hai điểm cùng nhìn đoạn NC dưới một góc vuông nên hình chóp nội tiếp mặt cầu tâm J là trung điểmNC, bán kính:
Chọn A.
Câu 10:	Cho hình chóp có đáy là hình vuôngcạnh bằng Đường thẳng vuông góc đáy Gọi H là hình chiếu của A trên đường thẳng Bán kính mặt cầu ngoại tiếp tứ diện có giá trị nào sau đây?
A.	B.	
C.	D.
Hướng dẫn giải:
Gọi 
Vì là hình vuông nên 
Ta có
Lại có Suy ra nên tam giác vuông tại H
và có O là trung điểm cạnh huyền AC nên suy ra 
Từ 
Chọn C.
Câu 11:	Cho hình chóp tứ giác đều có cạnh bên bằng cạnh đáy bằng . Khi đó mặt cầu nội tiếp hình chóp có bán kính bằng:
A.	B.	C.	D.
Hướng dẫn giải:
Gọi là tâm của hình vuông .
Ta có là trục đường tròn ngoại tiếp đáy.
Gọi là trung điểm của và là chân đường phân giác trong của góc .
Suy ra là tâm của mặt cầu nội tiếp hình chóp, bán kính .
Ta có 
Dựa vào tính chất của đường phân giác ta có:
Chọn B.
Câu 12:	Cho hình chóp có đáy là tam giác vuông tại C và Mặt phẳng vuông góc với đáy, Bán kính mặt cầu ngoại tiếp hình chóp là:
A.	B.	
C.	D.
Hướng dẫn giải:
Gọi M trung điểm AB, suy ra và 
Do đó, là trục của tam giác 
Trong mặt phẳng kẻ đường trung trực của đoạn SB cắt SM tại I. Khi đó I là tâm mặt cầu ngoại tiếp hình chóp , bán kính 
Ta có: .
Trong tam giác vuông ta có 
Ta có Suy ra 
Chọn C.
Câu 13:	Cho hình chóp có đáy là hình vuôngcạnh bằng Đường thẳng vuông góc với đáy Gọi M trung điểm SC, mặt phẳng đi qua hai điểm A và M đồng thời song song với BD cắt lần lượt tại Bán kính mặt cầu đi qua năm điểm nhận giá trị nào sau đây?
A.	B.	C.	D.
Hướng dẫn giải:
Mặt phẳng song song với BD cắt SB, SD lần lượt tại E, F nên cân tại A, trungtuyến AM nên 
Ta có Do đó 
Từ suy ra .
Lại có: 
Từ suy ra 
Tương tự ta cũng có Do đó nên 5 điểm cùng thuộc mặt cầu tâm I là trung điểm của SA, bán kính 
Câu 14:	Cho khối chópcó ; tam giác cân tại ,;. Gọi lần lượt là hình chiếu của lên . Tính bán kính mặt cầu đi qua 5 điểm .
A.	B.
C.	D.Không tồn tại mặt cầu như vậy
Hướng dẫn giải:
Gọi là tâm đường tròn ngoại tiếp tam giác và là một đường kính của đường tròn .
Tam giác vuông tại , suy ra: mà nên .
Ta lại có: .
Suy ra tam giác vuông tại , suy ra: .
Tương tự như trên ta cũng có: .
Vậy thì ,
do đó 5 điểm cùng nằm trên một mặt cầu(đpcm).
Bán kính của mặt cầu cũng là bán kính đường tròn ngoại tiếp tam giác .
Áp dụng định lý cos ta có: .
Áp dụng định lý sin ta có: .
Chọn B.
Câu 15:	Cho lăng trụ có . Cạnh bên . Bán kính mặt cầu ngoại tiếp tứ diện bằng
A..	B..	C..	D..
Hướng dẫn giải:
ChọnB.
Dễ thấy tâm mặt cầu ngoại tiếp tứ diện cũng là tâm mặt cầu ngoại tiếp khối lăng trụ đứng đã cho.
Gọi là tâm đường tròn ngoại tiếp tam giác .
Đường thẳng qua vuông góc với cắt mặt phẳng trung trực của tại . Khi đó là tâm mặt cầu ngoại tiếp.
Mặt khác 
Ta có:do đó .
Câu 16:	Cho lăng trụ đứng có đáy là tam giác vuông tại góc bằng Góc giữa đường thẳng và mặt phẳng bằng Bán kính mặt cầu ngoại tiếp tứ diện bằng:
A.	B.	C.	D.
Hướng dẫn giải:
Ta có 
Trong tam giác ABC, ta có 
Trong ta có .
Gọi N là trung điểm AC,
suy ra N là tâm đường tròn
ngoại tiếp 
Gọi I là trung điểm 
suy ra 
Do đó là trục của ,
suy ra 
Hơn nữa, tam giác vuông tại A có I là trung điểm nên 
Từ , ta có hay I là tâm của mặt cầu ngoại tiếp hình chóp với bán kính 
Chọn B.
Câu 17:	Cho hình chóp có đáy là tam giác đều cạnh hình chiếu vuông góc của đỉnh S trên mặt phẳng là trung điểm H của cạnh Góc giữa đường thẳng SA và mặt phẳng bằng Gọi G là trọng tâm tam giác là bán kính mặt cầu có tâm G và tiếp xúc với mặt phẳng Đẳng thức nào sau đây sai?
A.	B.	C.	D.
Hướng dẫn giải:
Ta có 
Tam giác đều cạnh nên 
Trongtam giác vuông SHA, ta có
Vì mặt cầu có tâm G và tiếp xúc với nên bán kính mặt cầu 
Ta có Gọi M, E lần lượt là trung điểm 
 Suy ra và 
Gọi K là hình chiếu vuông góc của H lên SE, suy ra 
Ta có 
Từ 
Trong tam giác vuông SHE, ta có Vậy 
Chọn D.
Câu 18:	Cho hình chóp có SA vuông góc với đáy, Đáy là hình thang vuông tại và Gọi E là trung điểm Tính bán kính mặt cầu ngoại tiếp hình chóp 
A.	B.	C.	D.
Hướng dẫn giải:
Gọi H là trung điểm của CD và là đường thẳng đi qua H và vuông góc với đáy. Gọi I và R là tâm và bán kính mặt cầu ngoại tiếp Suy ra I thuộc	D.Đặt Trong mp kẻ đường thẳng đi qua I và song song với AH cắt AS tại K.
Ta có: 
Suy ra: 
Vậy bán kính mặt cầu bằng 
Chọn C.
Câu 19:	Cho tứ diện có đáy là tam giác vuông tại với , . Hình chiếu của trùng với tâm đường tròn nội tiếp tam giác . Biết , bán kính mặt cầu ngoại tiếp hình chóp là
A..	B..	C..	D..
Hướng dẫn giải:
ChọnA.
Gọi là bán kính đường tròn nội tiếp tam giác . Tính được .
Tính được và .
Tam giác vuông tại suy ra 
Gọi là trung điểm của và là trục đường tròn ngoại tiếp tam giác .
Gọi là tâm mặt cầu ngoại tiếp . Suy ra .
Ta có:
.
Suy ra .
Câu 20:	Cho hình chóp có , , , . Gọi , lần lượt là hình chiếu vuông góc của lên , . Tính bán kính mặt cầu ngoại tiếp hình chóp theo , , 
A.	B.
C.	D.
Hướng dẫn giải:
Chọn C.
Gọi lần lượt là trung điểm của và .
Tam giác vuông tại nên chính là tâm đường
tròn ngoại tiếp tam giác , suy ra trục tâm đường tròn
ngoại tiếp tam giác chính là đường trung trực
 của (xét trong mp ).
Tam giác vuông tại nên chính là tâm đường
tròn ngoại tiếp tam giác , suy ra trục tâm đường tròn
ngoại tiếp tam giác chính là đường trung trực
 của (xét trong mp ).
Gọi thì là tâm đường tròn ngoại tiếp tam giác và cách đếu các điểm nên là tâm mặt cầu ngoại tiếp .
Gọi là bán kính mặt cầu ngoại tiếp thì chính là bán kính đường tròn ngoại tiếp tam giác.
Ta có .
ỨNG DỤNG THỰC TẾ
Câu 1:	Người ta bỏ quả bóng bàn cùng kích thước vào một chiếc hộp hình trụ có đáy bằng hình tròn tròn lớn của quả bóng bàn và chiều cao bằng lần đường kính của quả bóng bàn. Gọi là tổng diện tích của quả bóng bàn, là diện tích xung quanh của hình trụ. Tỉ số là:
A..	B.	C..	D.
Hướng dẫn giải: 
Chọn C.
Gọi bán kính của quả bóng bàn là 
Ta có chiều cao h của hình trụ bằng 5 lần đường kính của quả bóng bàn nghĩa là:
Khi đó:
Và 
Vậy:.
Câu 2:	Một công ty sản xuất một loại cốc giấy hình nón có thể tích với chiều cao là và bán kính đáy là để lượng giấy tiêu thụ là ít nhất thì giá trị của là:
A..	B..	C..	D..
Hướng dẫn giải: 
Chọn B
Thể tích của cốc: 
Lượng giấy tiêu thụ ít nhất khi và chỉ khi diện tích xung quanh nhỏ nhất.
 (theo BĐT Cauchy)
 nhỏ nhất .
Câu 3:	Một phễu đựng kem hình nón bằng giấy bạc có thể tích (cm3) và chiều cao là 4cm. Muốn tăng thể tích kem trong phễu hình nón lên 4 lần, nhưng chiều cao không thay đổi, diện tích miếng giấy bạc cần thêm là.
A..	B..
C..	D.
Hướng dẫn giải:
Gọi R1 là bán kính đường tròn đáy hình nón lúc đầu; h1 là chiều cao của hình nón lúc đầu.
Gọi R2 là bán kính đường tròn đáy hình nón sau khi tăng thể tích; h2 là chiều cao của hình nón sau khi tăng thể tích.
Ta có: 
Diện tích xung quanh hình nón lúc đầu: 
Diện tích xung quanh hình nón sau khi tăng thể tích: 
Diện tích phần giấy bạc cần tăng thêm là: 
Chọn A.
Câu 4:	Một cái phễu có dạng hình nón, chiều cao của phễu là ( Hình 1) Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu lả . Nếu bịt kín mi