Bảng đặc tả đề kiểm tra Cuối Học kì II môn Toán Lớp 11 trường THPT Ngô Quyền

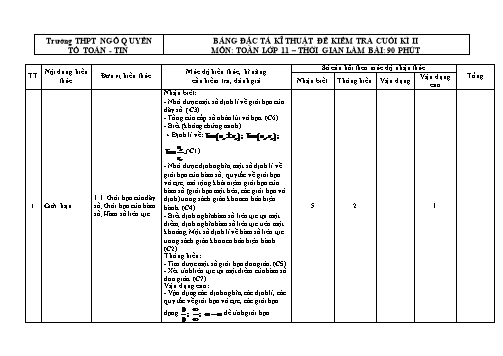
Trường THPT NGÔ QUYỀN
TỔ TOÁN - TIN
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA CUỐI KÌ II
MÔN: TOÁN LỚP 11 – THỜI GIAN LÀM BÀI: 90 PHÚT
TT
Nội dung kiến thức
Đơn vị kiến thức
Mức độ kiến thức, kĩ năng 
cần kiểm tra, đánh giá
Số câu hỏi theo mức độ nhận thức
Tổng
Nhận biết
Thông hiểu
Vận dụng 
Vận dụng cao
1
Giới hạn
1.1. Giới hạn của dãy số; Giới hạn của hàm số; Hàm số liên tục.
Nhận biết:
- Nhớ được một số định lí về giới hạn của dãy số. (C3)
- Tổng của cấp số nhân lùi vô hạn. (C6)
- Biết (không chứng minh)
 + Định lí về: (C1)
- Nhớ được định nghĩa; một số định lí về giới hạn của hàm số; quy tắc về giới hạn vô cực; mở rộng khái niệm giới hạn của hàm số (giới hạn một bên, các giới hạn vô định) trong sách giáo khoa cơ bản hiện hành. (C4)
- Biết định nghĩa hàm số liên tục tại một điểm; định nghĩa hàm số liên tục trên một khoảng; Một số định lí về hàm số liên tục trong sách giáo khoa cơ bản hiện hành. (C2)
Thông hiểu:
- Tìm được một số giới hạn đơn giản. (C5)
- Xét tính liên tục tại một điểm của hàm số đơn giản. (C7)
Vận dụng cao: 
- Vận dụng các định nghĩa, các định lí, các quy tắc về giới hạn vô cực, các giới hạn dạng để tính giới hạn.
- Chứng minh được một phương trình có nghiệm dựa vào định lí về hàm số liên tục. (C3a)
5
2
1
2
Đạo hàm
2.1. Định nghĩa và ý nghĩa của đạo hàm
Nhận biết: 
- Biết ý nghĩa vật lí và hình học của đạo hàm. (C8)
Thông hiểu: 
- Tính được đạo hàm của hàm lũy thừa, hàm đa thức bậc hai, bậc ba theo định nghĩa. (C9)
Vận dụng: 
- Lập được phương trình tiếp tuyến của đồ thị hàm số đa thức tại một điểm thuộc đồ thị đó. (C1)
- Biết tìm vận tốc tức thời của một chuyển động có phương trình 
Vận dụng cao:
- Lập được phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị đó. (C3b)
1
1
1
1
2.2. Quy tắc tính đạo hàm
Nhận biết: 
- Nhớ được đạo hàm của các hàm số (c10)
- Biết quy tắc tính đạo hàm của tổng, hiệu, tích thương các hàm số; hàm hợp và đạo hàm của hàm hợp. (c11, c12, c13, c14, c15)
Thông hiểu: 
- Tính được đạo hàm của số đơn giản. (c16, c17)
6
2
2.3. Đạo hàm của hàm số lượng giác
Nhận biết: 
- Biết được 
- Biết được đạo hàm của hàm số lượng giác. (c18, c19, c22)
Thông hiểu:
- Biết vận dụng trong một số giới hạn dạng đơn giản. (c20)
- Tính được đạo hàm của một số hàm số lượng giác đơn giản. (c21, c23)
3
3
2.4. Đạo hàm cấp hai
Thông hiểu: 
- Hiểu được định nghĩa, cách tính, ý nghĩa hình học và cơ học của đạo hàm cấp hai. 
- Tính được đạo hàm cấp hai của một hàm số. (c24)
- Tính được gia tốc tức thời của một chuyển động có phương trình (c25)
2
3
Vectơ trong không gian. Quan hệ vuông góc trong không gian.
3.1. Vectơ trong không gian
Nhận biết: 
- Nhớ được định nghĩa, các phép toán của vectơ trong không gian.
- Biết được quy tắc hình hộp để cộng vectơ trong không gian. Định nghĩa và điều kiện đồng phẳng của ba vectơ trong không gian. (c26)
1
3.2. Hai đường thẳng vuông góc
Nhận biết: 
Biết được:
-Nhớ được định nghĩa góc giữa hai vectơ trong không gian.
- Khái niệm vectơ chỉ phương của đường thẳng.
- Khái niệm góc giữa hai đường thẳng. (c27) 
- Khái niệm và điều kiện hai đường thẳng vuông góc với nhau. 
- Nhớ được điều kiện vuông góc giữa hai đường thẳng.
Thông hiểu: 
- Hiểu được tích vô hướng của hai vectơ. 
- Xác định được vectơ chỉ phương của đường thẳng; góc giữa hai đường thẳng trong các bài toán đơn giản. 
- Xác định được góc giữa hai vectơ trong không gian trong các bài toán đơn giản. 
- Chứng minh được hai đường thẳng vuông góc với nhau trong các bài toán đơn giản. (C28)
1
1
3.3. Đường thẳng vuông góc với mặt phẳng
Nhận biết: 
- Biết được định nghĩa và điều kiện để đường thẳng vuông góc với mặt phẳng. (C29)
- Biết được khái niệm phép chiếu vuông góc. 
- Biết được khái niệm mặt phẳng trung trực của một đoạn thẳng. 
Thông hiểu: 
- Biết cách chứng minh một đường thẳng vuông góc với một mặt phẳng, một đường thẳng vuông góc với một đường thẳng trong một số bài toán đơn giản. (c30, 31)
1
2
3.4. Hai mặt phẳng vuông góc
Nhận biết: 
- Biết được định nghĩa góc giữa hai đường mặt phẳng. 
- Biết được định nghĩa và điều kiện để hai mặt phẳng vuông góc. 
- Biết được định nghĩa và tính chất của hình lăng trụ đứng, lăng trụ đều, hình hộp đứng, hình hộp chữ nhật, hình lập phương. (C32)
- Biết được định nghĩa và tính chất của hình chóp đều và hình chóp cụt đều. 
Thông hiểu:
- Xác định được góc giữa hai mặt phẳng trong một số bài toán đơn giản.
- Biết chứng minh hai mặt phẳng vuông góc trong một số bài toán đơn giản. (C33) 
1
1
3.5. Khoảng cách 
Nhận biết:
- Biết định nghĩa khoảng cách từ một điểm đến một đường thẳng. (C34)
- Biết định nghĩa khoảng cách từ một điểm đến một mặt phẳng. 
- Biết định nghĩa khoảng cách giữa hai đường thẳng song song. 
- Biết định nghĩa khoảng cách giữa đường thẳng và mặt phẳng song song. 
- Biết định nghĩa khoảng cách giữa hai mặt phẳng song song. 
Thông hiểu: Trong các bài toán đơn giản: 
- Xác định được khoảng cách từ một điểm đến một đường thẳng. 
- Xác định được khoảng cách từ một điểm đến một mặt phẳng. (C35)
- Xác định được khoảng cách giữa đường thẳng và mặt phẳng song song. 
- Xác định được khoảng cách giữa hai mặt phẳng song song.
- Xác định được đường vuông góc của hai đường thẳng chéo nhau. 
Xác định được khoảng cách giữa hai đường thẳng chéo nhau.
Vận dụng: 
- Xác định được khoảng cách từ một điểm đến một đường thẳng. 
- Xác định được khoảng cách từ một điểm đến một mặt phẳng.
- Xác định được khoảng cách giữa đường thẳng và mặt phẳng song song. 
- Xác định được khoảng cách giữa hai mặt phẳng song song.
- Xác định được đường vuông góc của hai đường thẳng chéo nhau. 
-Xác định được khoảng cách giữa hai đường thẳng chéo nhau. (c2)
1
1
1
Tổng
20
15
2
2
39