Bài giảng Toán Lớp 10 - Bài 4: Đường tròn (Tiết 1) - Trường THPT Quang Trung

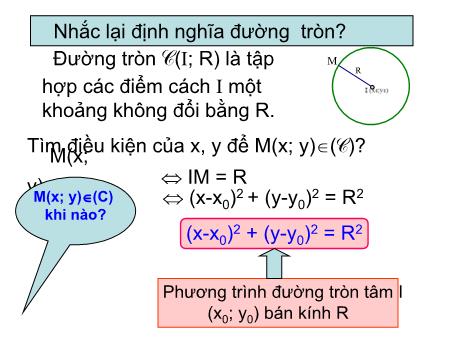
Nhắc lại định nghĩa đường tròn ? 
Phương trình đường tròn tâm I(x 0 ; y 0 ) bán kính R 
Đường tròn C ( I ; R) là tập hợp các điểm cách I một khoảng không đổi bằng R. 
R 
M 
Tìm điều kiện của x, y để M(x ; y) ( C )? 
M(x ; y) ( C ) 
(x-x 0 ) 2 + (y-y 0 ) 2 = R 2 
 (x-x 0 ) 2 + (y-y 0 ) 2 = R 2 
M(x ; y) ( C ) khi nào ? 
 IM = R 
§4. ĐƯỜNG TRÒN ( ti ết 1) 
Đường tròn tâm I ( x 0 ; y 0 ) bán kính R có phương trình : 
(x-x 0 ) 2 + (y-y 0 ) 2 = R 2 
(x- x 0 ) 2 + (y- y 0 ) 2 = R 2 
1. Phương trình đường tròn . 
Để viết pt đường tròn cần biết điều kiện gì ? 
Để viết pt đường tròn cần biết tọa độ tâm I và bán kính R. 
§4. ĐƯỜNG TRÒN 
Đường tròn tâm I ( x 0 ; y 0 ) bán kính R có phương 
trình : 
(x- x 0 ) 2 + (y- y 0 ) 2 = R 2 
1. Phương trình đường tròn . 
Ví dụ : Cho hai điểm A(3; - 4) và B(- 3; 4). 
	 a) Đường tròn tâm A và đi qua B có bán kính 
 R = AB 
a) Viết pt đường tròn tâm A và đi qua B 
b) Viết pt đường tròn đường kính AB 
Bài giải : 
Nên pt của đường tròn là : (x - 3) 2 +(y + 4) 2 = 100 
A 
B 
§4. ĐƯỜNG TRÒN 
Đường tròn tâm I ( x 0 ; y 0 ) bán kính R có phương 
trình : 
(x- x 0 ) 2 + (y- y 0 ) 2 = R 2 
1. Phương trình đường tròn . 
Ví dụ : Cho hai điểm A(3; - 4) và B(- 3; 4). 
a) Viết pt đường tròn tâm A và đi qua B 
b) Viết pt đường tròn đường kính AB 
Bài giải : 
b) Đường tròn đường kính AB có tâm là trung điểm của AB bán kính 
Nên phương trình đường tròn là : x 2 +y 2 = 25 
A 
B 
I 
Ta có:R = 5 ; trung điểm của AB là O(0;0) 
§4. ĐƯỜNG TRÒN 
Đường tròn tâm I ( x 0 ; y 0 ) bán kính R có phương 
trình : 
(x- x 0 ) 2 + (y- y 0 ) 2 = R 2 
1. Phương trình đường tròn . 
Đặc biệt : Đường tròn (O; R) có pt là : x 2 + y 2 = R 2 
Phương trình đường thẳng có nhiều dạng . Phương trình của đường tròn có những dạng nào ? 
Các nhóm thực hiện yêu cầu sau : 
Khai triển phương trình 
(x - x 0 ) 2 + (y - y 0 ) 2 = R 2 
Chuyển phương trình 
x 2 + y 2 +2ax + 2by + c = 0 về dạng (x - x 0 ) 2 +(y - y 0 ) 2 = R 2 
x 2 +y 2 -2x 0 x-2y 0 y+x 0 2 +y 0 2 -R 2 = 0 
 (x + a) 2 +(y + b) 2 = a 2 +b 2 -c (*) 
Có dạng : 
x 2 + y 2 +2ax + 2by + c = 0 
IM 2 
Với I (-a; -b) 
. 
Phương trình (*) là phương trình đường tròn thì a, b,c thoả mãn điều kiện gì ? 
2. Nhận dạng phương trình đường tròn 
Phương trình x 2 + y 2 +2ax + 2by + c = 0, với a 2 +b 2 - c >0, là phương trình của đường tròn tâm I ( -a; -b), bán kính 
§4. ĐƯỜNG TRÒN ( ti ết 1) 
Đường tròn tâm I ( x 0 ; y 0 ) bán kính R có phương trình : 
(x- x 0 ) 2 + (y- y 0 ) 2 = R 2 
1. Phương trình đường tròn . 
Phương trình x 2 + y 2 +2ax + 2by + c = 0, với a 2 +b 2 - c >0, là phương trình của đường tròn tâm I ( -a; -b), bán kính 
Chọn đáp án đúng cho các câu sau 
1)Tâm của đường tròn x 2 + y 2 + 2x +2y -2 = 0 là : 
	A. (1; 1)	 B. (-1; 1)	C.(-1; -1)	D. (1; -1) 
2)Tâm của đường tròn x 2 + y 2 - 2x +2y -2 = 0 là : 
	A. (1; 1)	B. (-1; 1)	C.(-1; -1)	D. (1; -1) 
3)Tâm của đường tròn 2x 2 + 2y 2 - 4x - 8y -2 = 0 là : 
	A. (2; 4)	B. (1; 2)	C.(-1; -1)	D. (-2; -1) 
Trong mỗi trường hợp hãy xác định bán kính của đường tròn đó . 
R = 2 
R = 2 
Trong các phương trình sau , phương trình nào là phương trình của đường tròn ? 
Đ 
S 
Đ 
S 
S 
Chú ý : Phương trình đường tròn dạng x 2 + y 2 +2ax + 2by + c = 0 
thì hệ số của x 2 và y 2 phải bằng nhau . 
Phương trình x 2 + y 2 +2ax + 2by + c = 0, với a 2 +b 2 - c >0, là phương trình của đường tròn tâm I ( -a; -b), bán kính 
Phương trình x 2 + y 2 +2ax + 2by + c = 0, với a 2 +b 2 - c >0, là phương trình của đường tròn tâm I ( -a; -b), bán kính 
Ví dụ : 
	 Viết phương trình đường tròn đi qua ba điểm 
	A (-2; -1), B (-1; 4), C (4; 3). 
(x-x 0 ) 2 + (y-y 0 ) 2 = R 2 
Nêu cách giải cách giải của bài toán . 
- Xác định toạ độ tâm I và bán kính R. 
Cách khác : Xác định các hệ số a, b, c. 
IA = IB = IC 
Vì đường tròn đi qua 3 điểm A, B, C nên 
toạ độ của chúng thoả mãn pt đường tròn . 
Ví dụ : 
	 Viết phương trình đường tròn đi qua ba điểm 
	A (-2; -1), B (-1; 4), C (4; 3). 
Bài giải : Gọi I (a; b) và R là tâm và bán kính của đường tròn đi qua 3 điểm A, B, C. 
Từ điều kiện IA = IB = IC ta có hệ phương trình : 
Giải hệ phương trình ta có a = 1; b= 1. 
Khi đó R 2 = IM 2 = 13. Phương trình đường tròn cần tìm là : 
(x - 1) 2 + (y - 1) 2 = 13 
Ví dụ : Viết phương trình đường tròn đi qua ba điểm 
	A (-2; -1), B (-1; 4), C (4; 3). 
Bài giải : Gọi I (a; b) và R là tâm và bán kính của đường tròn đi qua 3 điểm A, B, C. 
Từ điều kiện IA = IB = IC ta có hệ phương trình : 
Cách khác : 
Giải hệ phương trình ta có a = 1; b= 1. 
Khi đó R 2 = IM 2 = 13. Phương trình đường tròn cần tìm là : (x - 1) 2 + (y - 1) 2 = 13 
Giả sử pt đường tròn có dạng x 2 + y 2 +2ax + 2by + c = 0 . 
Do A, B, C thuộc đường tròn nên ta có hệ pt: 
phương trình đường tròn cần tìm là : x 2 + y 2 -2x -2y -11 = 0 
Thay a = -1, b= -1, c= -11 vào pt trên ta có : 
Phương trình x 2 + y 2 +2ax + 2by + c = 0, với a 2 +b 2 - c >0, là phương trình của đường tròn tâm I ( -a; -b), bán kính 
C ủng cố 
Đường tròn tâm I ( x 0 ; y 0 ) bán kính R có phương trình : 
(x- x 0 ) 2 + (y- y 0 ) 2 = R 2 
1. Phương trình đường tròn . 
2. Bài tập : 
	 - Xác định được tâm và bán kính của đường tròn . 
	- Viết được pt đường tròn 
	- Bài tập về nhà : 21, 23, 24, 25-SGK trang 95 
BÀI HỌC KẾT THÚC  CẢM ƠN CÁC THẦY CÔ VÀ CÁC EM HỌC SINH ĐÃ THEO DÕI